Frequently Asked Questions¶
What do I do to test convergence?¶
The best way to make sure that your GME computation is converged is to increase the parameters controlling the precision of the simulation until you no longer see change in the eigenmodes of interest. We recommend doing this in the following order:
- First, make sure you have set a high enough
gmax, which is defined upon initialization ofGuidedModeExp. - Then, increase the number of guided bands included in the simulation by
adding more indexes to the
gmode_indslist supplied toGuidedModeExp.run(). Note that after including more modes ingmode_inds, you should test again the convergence w.r.t.gmax. - If your bands look particularly weird and discontinuous, there might be an
issue in the computation of the guided modes of the effective homogeneous
structure (the expansion basis). Try decreasing
gmode_stepsupplied inGuidedModeExp.run()to1e-3or1e-4and see if things look better.
Finally, note that GME is only an approximate method. So, even if the simulation is converged with respect to all of the above parameters but still produces strange results, it might just be that the method is not that well-suited for the structure you are simulating. We’re hoping to improve that in future version of legume!
How do I incorporate symmetry?¶
The expansion basis in the GME consists of the guided modes of an effective homogeneous
structure. These can be classified as TE/TM, where in our notation the reference
plane is the slab plane. The guided modes alternate between TE and TM, such
that gmode_inds = [0, 2, 4, ...] are TE and gmode_inds = [1, 3, 5, ...] are
TM. However, this classification is often broken by the photonic crystal
permittivity.
For gratings (permittivity is periodic in one direction and homogeneous in the other), the TE/TM classification holds. You can selectively compute the modes by supplying gmode_inds with either only even or only odd numbers.
For photonic crystals with a mirror plane, like a single slab with symmetric
claddings, the correct classification of modes is with respect to reflection in
that plane. The positive-symmetry guided modes are
gmode_inds = [0, 3, 4, 7, 8, ...], while the negative-symmetry modes are
gmode_inds = [1, 2, 5, 6, 9, 10, ...]. Low-frequency positive-symmetry
modes that are mostly fromed by the gmode_inds = 0 guided band are
sometimes referred to as quasi-TE, and low-frequency negative-symmetry
modes that are mostly formed by the gmode_inds = 1 guided band are
sometimes referred to as quasi-TM.
Without any mirror planes, all the guided modes are generally mixed. There can still be symmetry if the k-vector points in a high-symmetry direction, but there is currently no way to take advantage of that in legume.
When should I use approximate gradients?¶
When running GME with the autograd backend, one of the run() options
you can specify is 'gradients' = {'exact' (default), 'approx'}. The
approximate option could be faster in some cases, and could actually still
be exact in some cases. This is the high-level computational graph of the
guided-mode expansion:
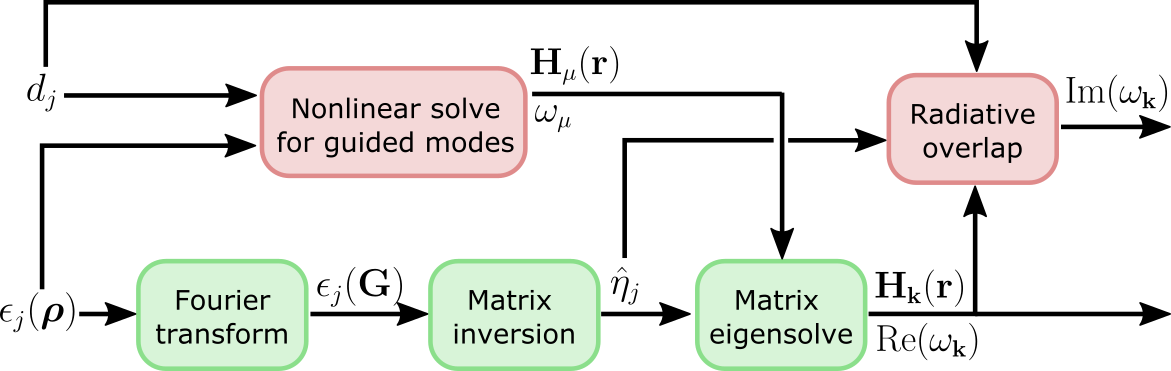
The 'approx' option discards the gradient due to the top path in this
graph, i.e. the gradient due to the changing basis. Only the gradient from the
diagonalization path is included. Here are some rules of thumb on what to use:
- If you’re optimizing hole positions, or more generally parameters that don’t
change the average permittivity, you’re in luck! In this case, the
'approx'gradients should actually be exact! - If you’re optimizing dispersion (real part of eigenfrequencies), you could try using
'approx'gradients, as they might be within just a few percent of the exact ones. - If you’re optimizing loss rates or field profiles
and/or if your parameters include the layer thicknesses, then the
'approx'gradients could be significantly off,'exact'is recommended (and is the default).
How can I learn more about the method?¶
Our manuscript gives a lot of detail both on the guided-mode expansion method and on our differentiable implementation. See Minkov et al., …
How should I cite legume?¶
If you find legume useful for your research, we would apprecite you citing our paper. For your convenience, you can use the following BibTex entry:
@article{legume,
title = {legume},
author = { ... },
year = {2020},
month = feb,
volume = { ... },
pages = { ... },
doi = { ... },
journal = { ... },
number = { ... }
}
Who made that awesome legume logo?¶
The legume logo was designed by Nadine Gilmer. She is also behind the logos for our angler and ceviche packages.